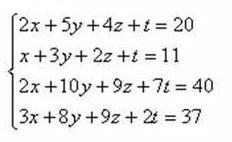Всем привет! Сегодня я покажу вам, как решать уравнения в Excel. Мы рассмотрим примеры с системными и квадратными уравнениями. Если у вас возникнут какие-то вопросы – пишите в комментариях, и команда портала WiFiGiD.RU постарается вам помочь.
Вариант 1: Матрицы
Давайте посмотрим, как в Экселе решить систему уравнений с несколькими неизвестными. Для этого мы будем использовать матричный метод. Давайте покажу, на примере:
Читаем – как вставить формулу в Эксель.
- Будем решать вот такую систему уравнений.
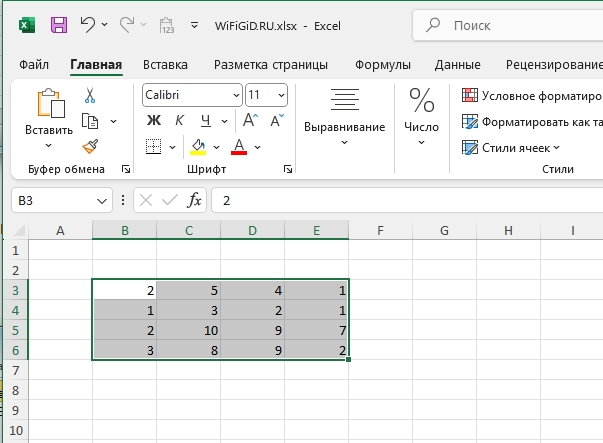
- Выписываем коэффициенты в виде матрицы. Обратите внимание, что если коэффициента в одном из уравнения нет, то записываем ноль (0).
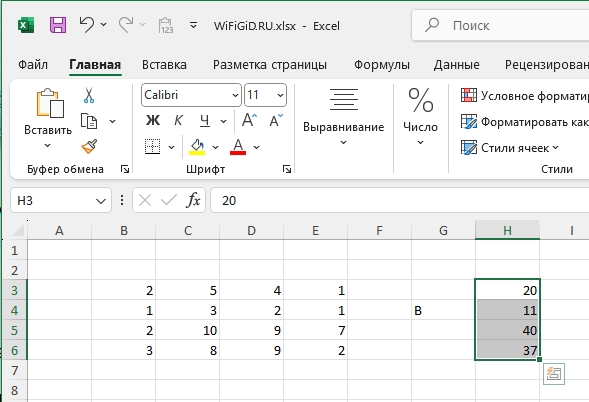
- Теперь отдельно выписываем результаты вычисления каждого уравнения.
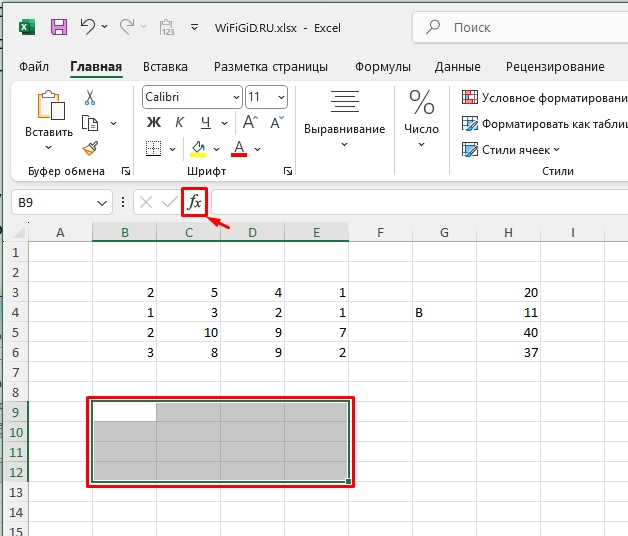
- Нам нужно получить обратную матрицу этой. Выделяем область пустых ячеек точно такого же размера, как исходная матрица.
- Жмем по кнопке «Вставить функцию».
- В «Категории» – «Математические» – указываем «МОБР» и жмем «ОК».
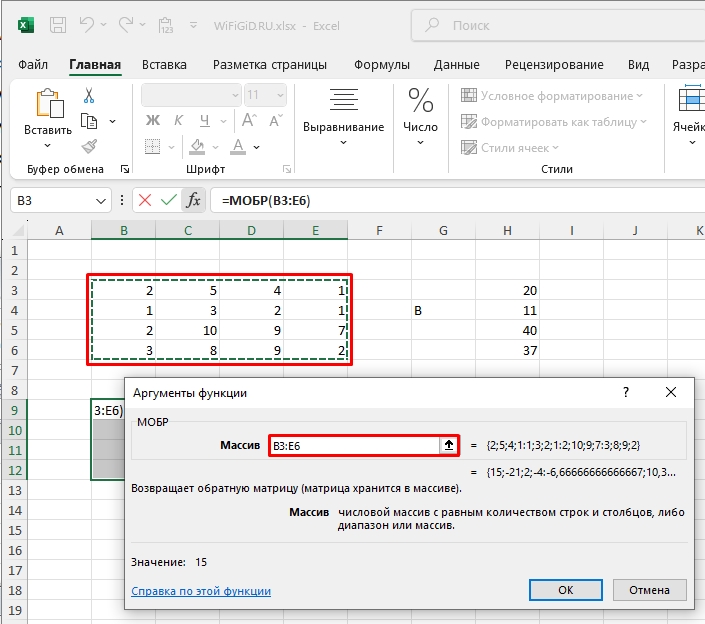
- Выделяем ячейки нашей первичной матрицы. ОЧЕНЬ ВАЖНО – нужно не нажимать по кнопке «ОК». Для работы с матрицами и массивами данных лучше использовать сочетание клавиш:
Ctrl + Shift + Enter
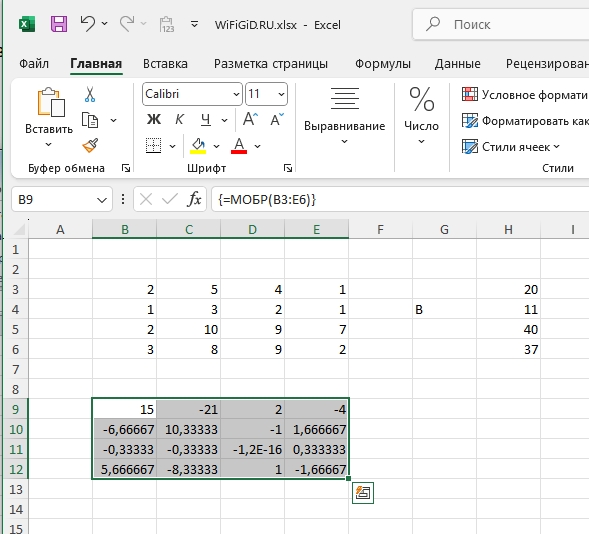
- Обратная матрица у нас есть.
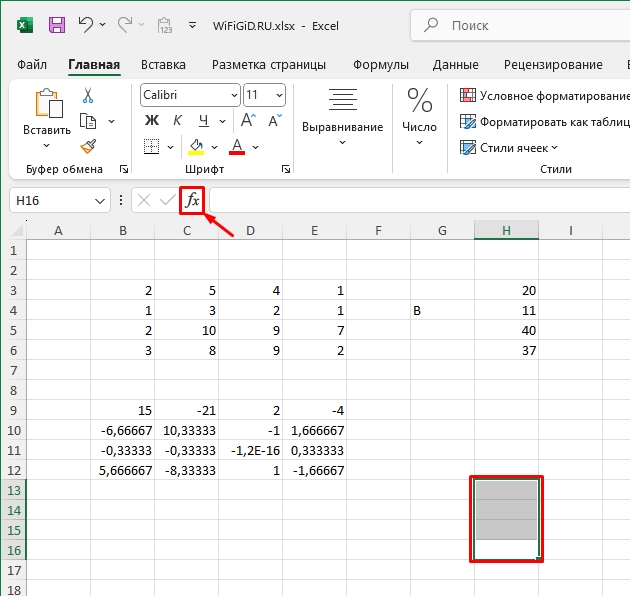
- Теперь нужно их перемножить, чтобы получить результат. Для этого выделаем ячейки, по количеству неизвестных (и уравнений-строк). Вставляем функцию.
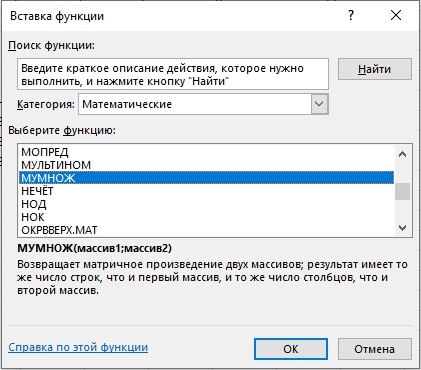
- Находим «МУМНОЖ».
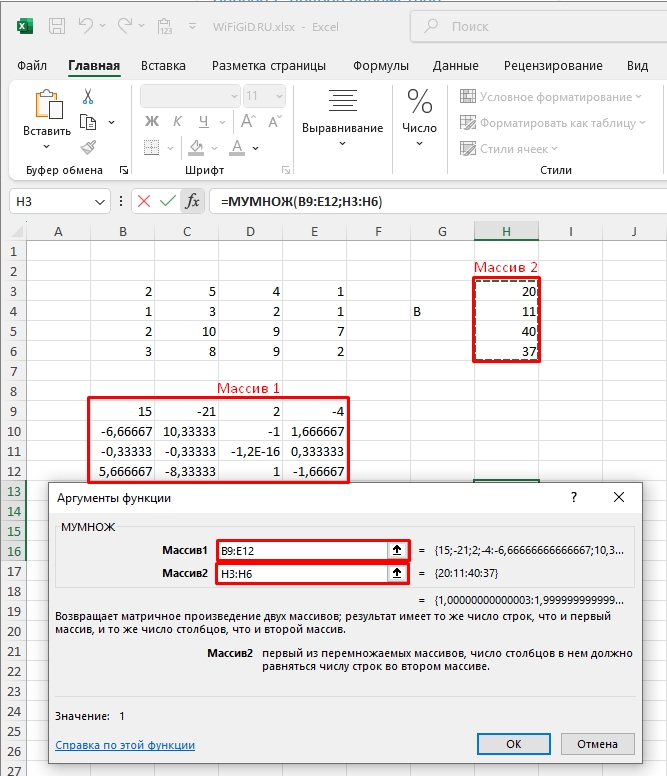
- В «Массив1» выделяем ячейки обратной матрицы. В «Массив2» – указываем результаты вычислений каждой из уравнений. В конце не забываем жать:
Ctrl + Shift + Enter
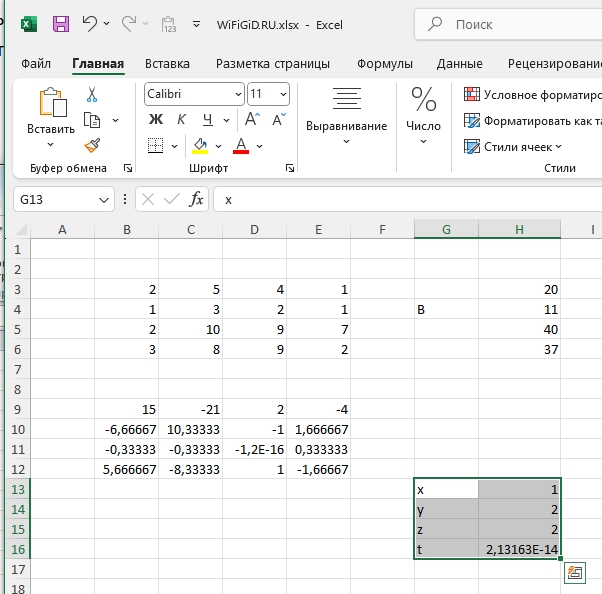
- Вот такие результаты мы получили по каждому неизвестному.
Вариант 2: Подбор
В качестве примера мы возьмем квадратное уравнение, и с помощью функции подбора параметров, попробуем найти одно неизвестное.
Читаем – как построить умную таблицу в Excel.
- Вот наш пример.
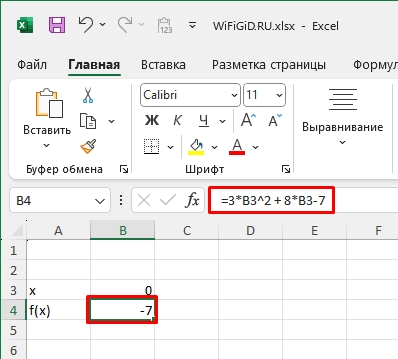
- В поле «x» – выводим 0.
- В качестве функции «f(x)» – указываем полный расчет. В итоге мы должны получить -7 в ответе.
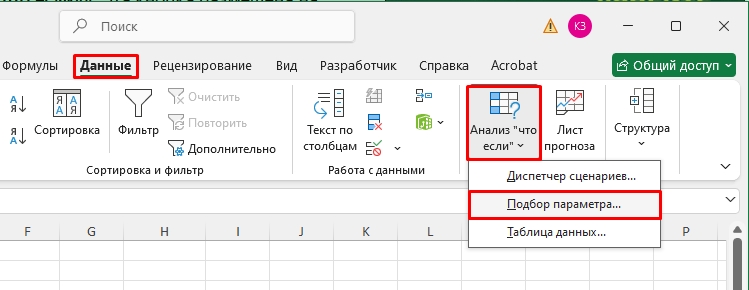
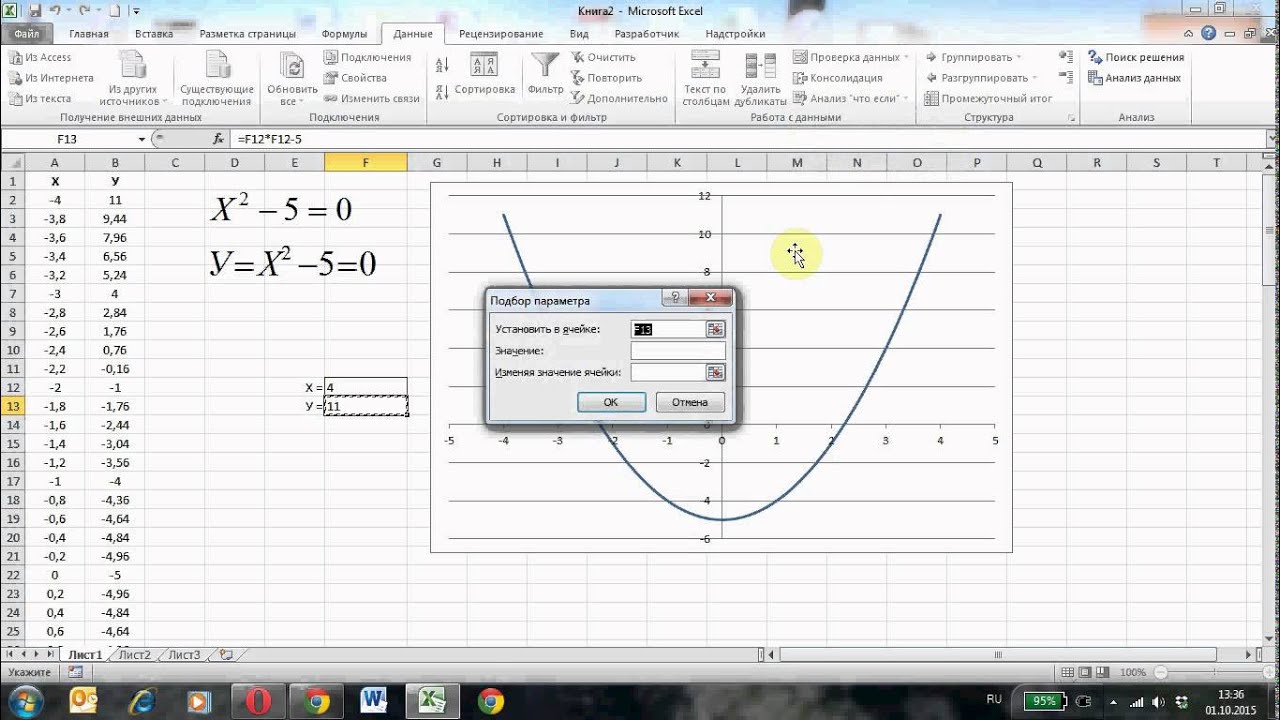
- Переходим во вкладку «Данные».
- Находим кнопку «Анализ (что если)» – «Подбор параметров».
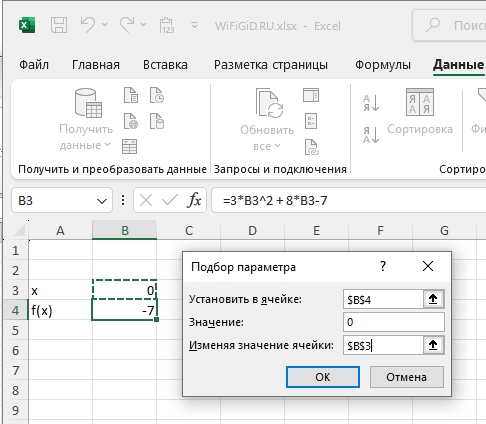
- А теперь заполняем строчки:
Установить в ячейке – выбираем ячейку с выражением «f(x)».
Значение – ставим ноль (0).
Изменяя значение ячейки – ставим ячейку значения «x».
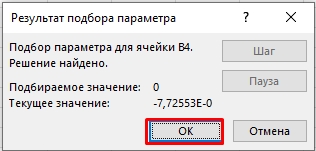
- После того как вы нажмете «ОК» начнется подбор. В конце еще раз жмем «ОК».
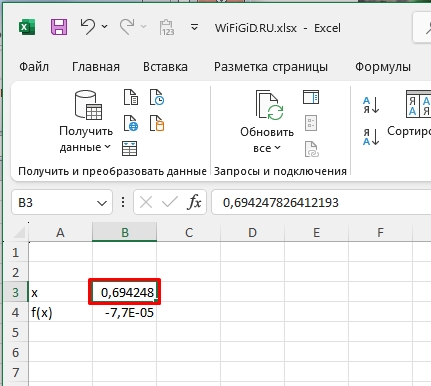
- Результат X будет находиться в соответствующей ячейке.
Вариант 3: метод Крамера
Для примера я взял все тот же пример, который мы использовали в первой главе.
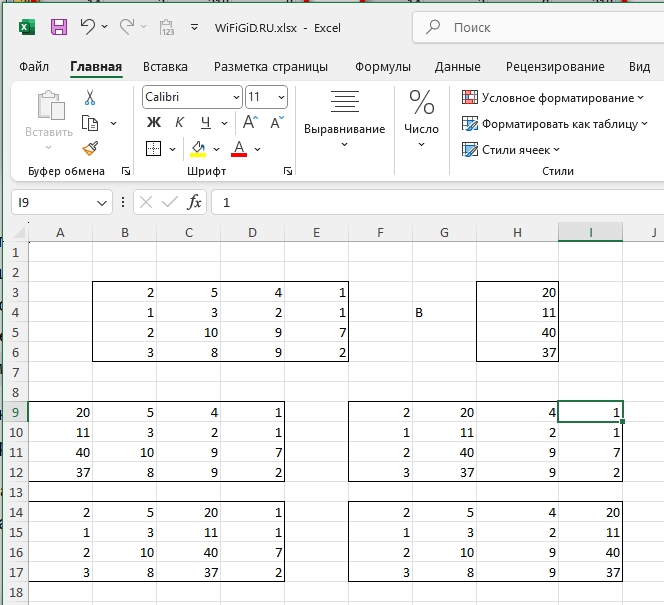
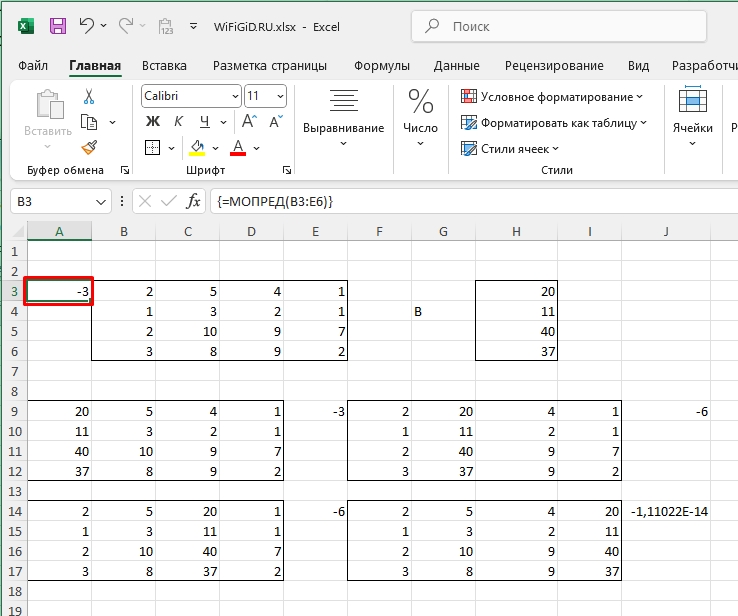
- Сначала строим матрицу и результаты вычисления каждого уравнения.
- Далее нам нужно построить 4 матрицы, где строки поочередно заменяются на результаты (B) столбца.
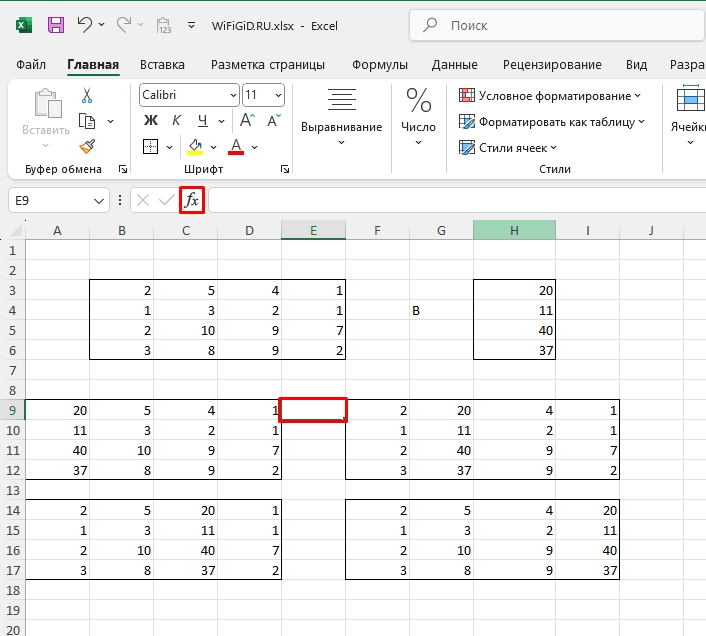
- Теперь для каждой из 4 таблицы нужно высчитать определители. Выбираем любую ячейку рядом и вставляем функцию.
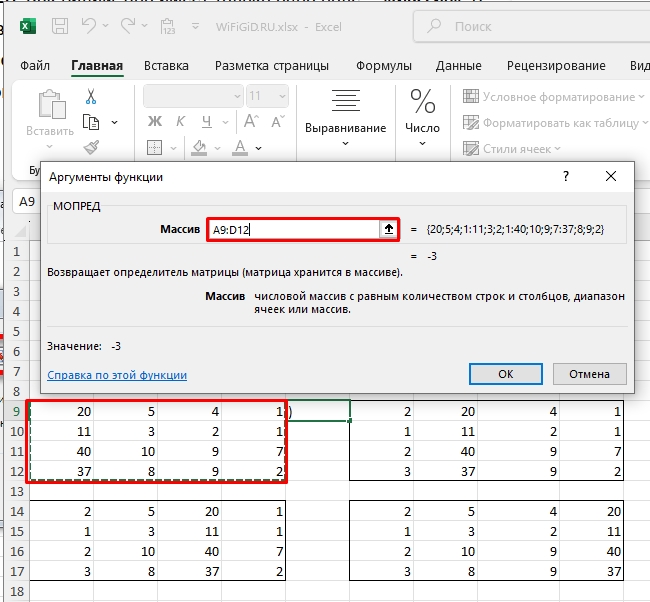
- Находим функцию «МОПРЕД» и выделяем нашу матрицу.
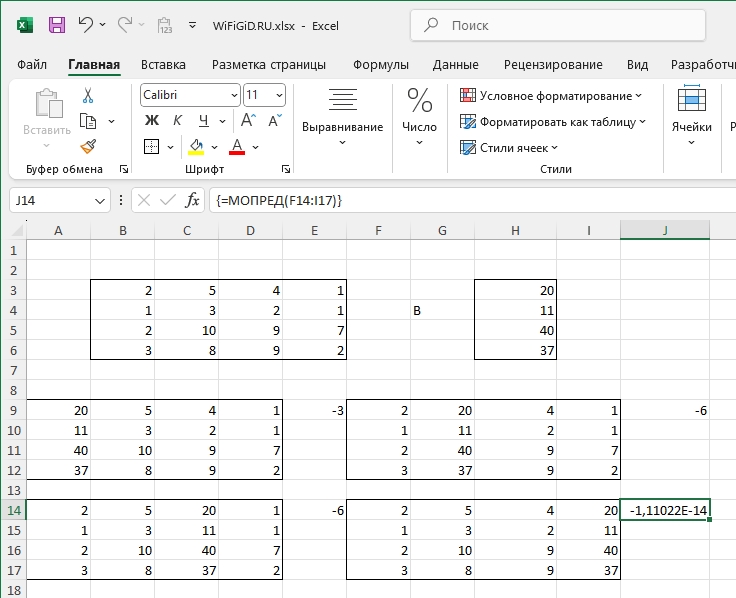
- Высчитываем определители для каждой матрицы. ОЧЕНЬ ВАЖНО – дальнейший расчет может быть только в том случае, если все определители отличны от нуля. Если хотя бы один равен нулю, то метод Крамера нам не подходит.
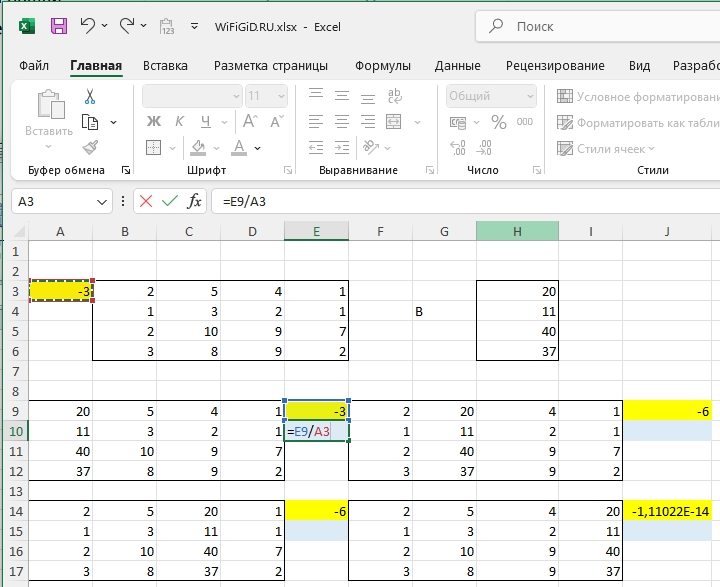
- Аналогично по формуле «МОПРЕД» рассчитайте определитель для основной (первичной) матрицы.
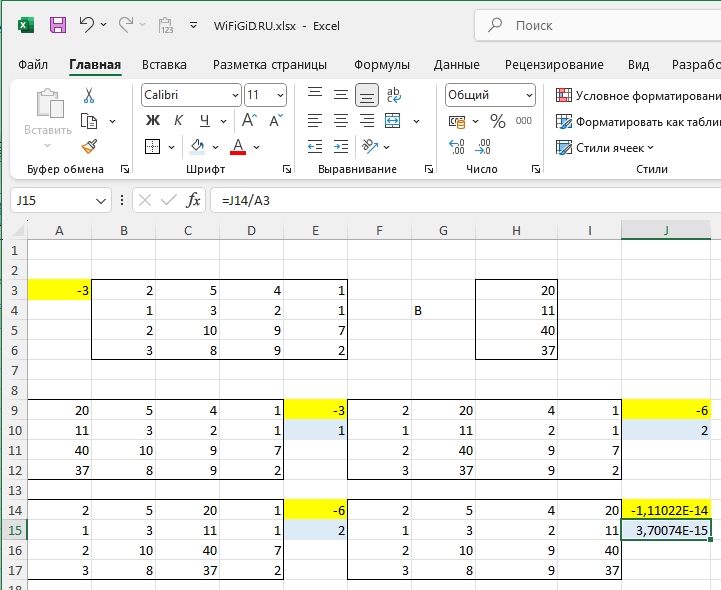
- Чтобы найти значение неизвестных, нам нужно разделить определитель выбранной матрицы на определитель исходной. Выполняем данный расчет для каждой матрицы.
- Таким образом мы получили результаты значений всех неизвестных.